
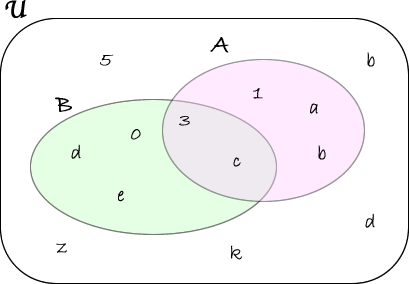
Verranno introdotti i seguenti contenuti
1) concetto di insieme,
2) come si rappresenta,
3) esempi di insieme finito e infinito, insieme vuoto,
4) inclusione di insiemi,
5) unione di insiemi,
6) intersezione di insiemi,
7) intersezione di insiemi,
8) differenza tra insiemi,
9) insieme complementare.
10) Operatori booleani e operazioni insiemistiche
Competenze degli alunni
saper rappresentare gli insiemi nelle tre modalità,
essere in grado di stabilire se un insieme è incluso in un altro,
saper determinare l'unione, l'intersezione e la differenza tra insiemi,
- saper determinare l'insieme complementare di un insieme.
- saper utilizzare gli operatori booleani nella realtà
Prerequisiti richiesti
non sono richiesti prerequisiti particolari
Tempo - scuola
n° 6 ore di lezione/attività.

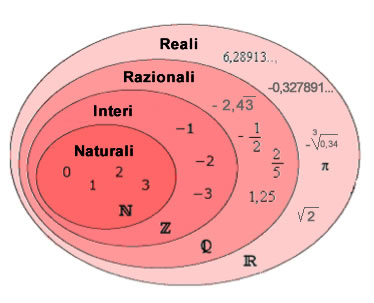
Verranno introdotti i seguenti contenuti
1) le quattro operazioni nell'insieme dei numeri Naturali e proprietà,
2) le quattro operazioni nell'insieme dei numeri Interi e proprietà,
3) le quattro operazioni nell'insieme dei numeri Razionali e proprietà,
4) introduzione concettuale dell'insieme dei numeri Reali e proprietà.
Competenze da raggiungere
distinguere un numero e il suo insieme di appartenza,
essere in grado di trovare l'opposto e il reciproco di un numero,
essere in grado di operare con le quattro operazioni dando le opportune priorità nel caso di espressioni combinate,
- essere in grado di trovare i numeri mancanti all'interno di un'espressione.
Prerequisiti richiesti
Gli insiemi e le operazioni tra gli insiemi
Tempo - scuola
n° 15 ore di lezione/attività.

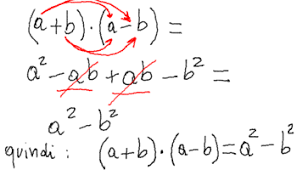
Verranno introdotti i seguenti contenuti
1) i monomi, le operazioni tra monomi,
2) i polinomi, somma algebrica tra polinomi
3) i polinomi, prodotto tra polinomi
4) espressioni con i polinomi
5) principali prodotti notevoli: differenza di quadrati, quadrato di binomio e cubo di binomio
Competenze da raggiungere
- Essere in grado di operare su espressioni algebriche contenenti monomi e polinomi.
- Riconosce li prodotti notevoli.
- Saper utilizzare i prodotti notevoli.
Saper usare le quattro operazioni tra numeri razionali
Tempo - scuola
n° 15 ore di lezione/attività.

Verranno introdotti i seguenti contenuti
1) concetto di equazione
2) concetto di disequazione,
3) i 2 principi delle equazioni,
4) i 2 principi delle disequazioni,
5) traduzione dal testo scritto alla forma di schemi, disegni,
6) comprensione del testo scritto,
7) traduzione dal testo scritto al linguaggio matematico,
8) risoluzione di semplici problemi di natura algebrica,
9) risoluzione di semplici problemi della vita di tutti i giorni,
10) risoluzione di semplici problemi di natura geometrica.
Competenze degli alunni
Essere in grado di risolvere equazioni, riconoscendo i principi applicati
Essere in grado di risolvere disequazioni, riconoscendo i principi applicati
Riuscire a tradurre un problema algebrico in linguaggio matematico
Riuscire a tradurre un problema della vita di tutti i giorni
Riuscire a tradurre un problema geometrico in linguaggio matematico
Riuscire a risolvere un problema algebrico, della vita di tutti i giorni, geometrico
Prerequisiti richiesti
- minimo comune multiplo
- utilizzo di frazioni
- operazione tra numeri razionali
- principali proprietà geometriche (somma angoli interni, angoli supplementari, complementari, calcolo perimetro e area triangoli e quadrilateri)
Tempo - scuola
n° 15 ore di lezione/attività.

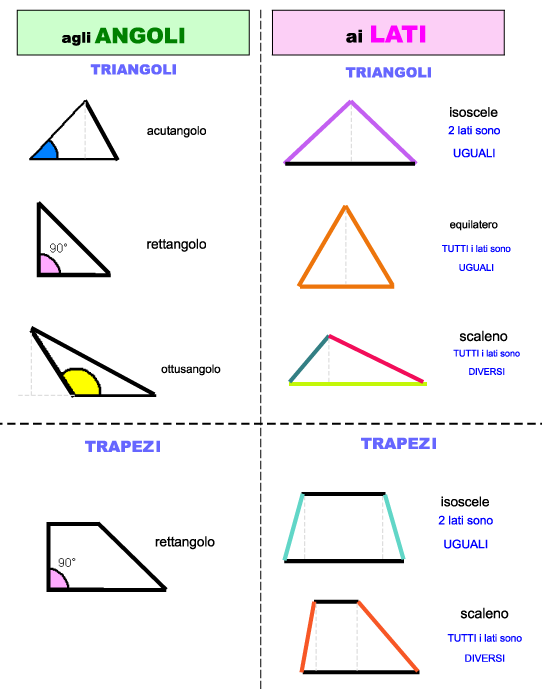
Contenuti
1) I primi elementi: punto, retta, piano, semiretta, segmento, angolo, circonferenza
2) Relazione tra segmenti
3) Relazione tra angoli
6) Asse e bisettrice
7) Rette parallele tagliate da una trasversale.
8) Triangoli e quadrilateri
9) I parallelogrammi
Competenze degli alunni
- Conoscere gli enti principali della geometria piana.
- Conoscere le principali relazioni tra segmenti e angoli.
- Leggere e interpretare le figure in termini di corrispondenze fra elementi.
- Applicare le proprietà principali studiate nei diversi contesti.
- Riconoscere le figure geometriche notevoli all'interno di una figura più complessa.
Tempo - scuola
n° 15 ore di lezione/attività.




